▣ 과도현상이란 특정 상태에서 다른 상태로 변화하는 과정을 말한다.
▣ 회로이론에서 과도현상이란 시간 t = 0을 기준으로 하여 t = 0 에서 어떤 현상의
변화가 나타난 후 정상상태(최종상태)가 나타나기 이전에 전압과 전류를 변화상태를
말한다.
▣ 과도현상을 이해하기 위해서는 먼저 소자의 특성을 알아야 한다.
◈ 저항 "R" : 저항은 에너지를 소비한다.
◈ 인덕턴스 "L" : 인덕턴스 "L"은 전류를 자속의 형태로 변화시켜 에너지를 저장한다.
에너지의 저장은 한번에 이루어지지 않고 시간을 갖고 연속적으로 서서
히 이루어진다.
⊙ 직류일 때 리액턴스 : XL = ωL = 2πfL = 0 ⇒ 단락상태 ∵ 직류일 때 f = 0
⊙ 전류 연속
◈ 커페시턴스 "C" : 커패시턴스 "C"는 전압을 전하의 형태로 에너지를 저항한다.
이것도 에너지를 한순간에 저장하지 않고 서서히 연속적으로 저장한다.
⊙ 직류일 때 커패시턴스 : XC = 1/ωC = 1/2πfL = ∞ ⇒ 개방상태 ∵ 직류일 때 f = 0
⊙ 전압 연속
1. 직류 R-L 직렬 회로
【 직류 R-L 직렬 회로】 직류 R - L 직렬 회로를 살펴 보자.
▣ 아래 회로와 같이 R만의 회로와 R-L회로를 비교해 보자.
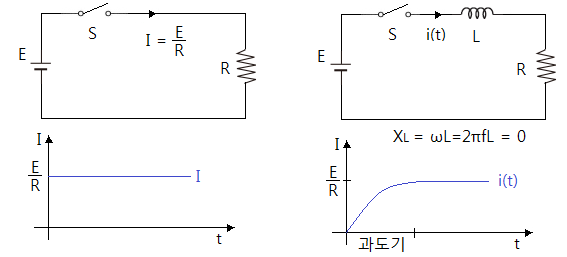
▣ R만의 직류회로에서는 스위치를 닫으면 바로 전류가 흐르게 된다. 오른 쪽 그림과 같이
R-L회로에서는 스위치를 닫으면 직류는 주파수(f=0)가 "0"이므로 리액턴스가 발생하
지 않아 최종적으로는 R만의 회로와 같이 전류가 흐르게 된다.
▣ 최종적으로는 직류회로에서 "L"은 리액턴스가 "0"이므로 리액터는 단락상태와 마찬가
지 이나 아주 짧은 시간을 확대하여 보면 전류의 시간적 변화를 관찰할 수 있다.
【 직류 R-C 직렬 회로】 직류 R - C 직렬 회로를 살펴 보자.
▣ 아래 회로와 같이 R만의 회로와 R-C회로를 비교해 보자.
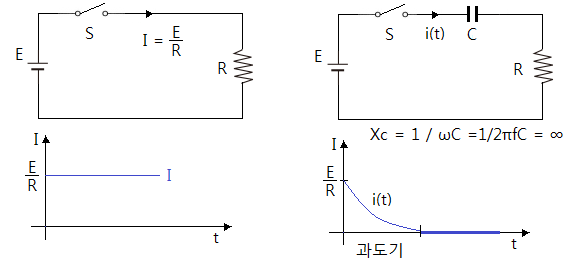
▣ R만의 회로에서는 스위치를 닫으면 바로 전류가 흐르게 된다. 오른 쪽 그림과 같이 R-C
회로에서는 스위치를 닫으면 직류는 주파수(f=0)가 "0"이므로 리액턴스가 "∞"가 되므
로 최종적으로는 전류가 흐르지 않는다.
▣ 그러나 초기 상태의 시간을 확대하여 보면 아주 짧은 시간이지만 전류가 흐르다가 서서
히 전류가 흐르지 않게 됨을 알 수 있다.
가. 직류 R - L 직렬 회로
▣ 직류 R - L 직렬 회로의 과도기를 상세하게 분석하여 보자.
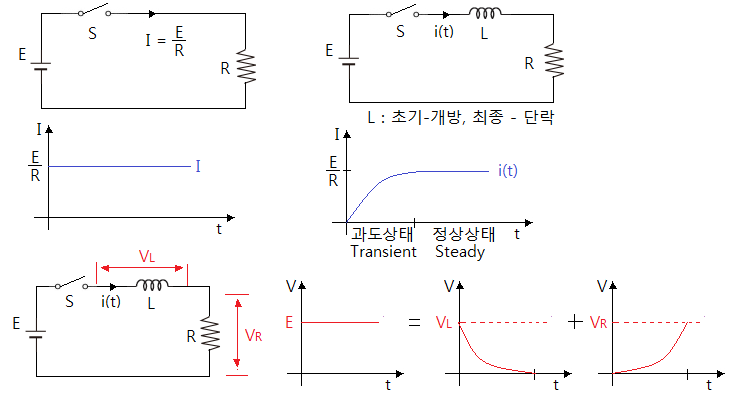
【 전압의 변화을 살펴 보면 】
▣ "L"에 발생하는 전압 VL은 처음에는 "L"은 개방상태와 마찬가지 이므로 리액턴스가
"∞"이므로 모든 전압이 "L"에 걸렸다가 점점 전압이 낮아져서 단락상태가 되면
리액턴스가 "0"이 되므로 전압은 "0"이 된다.
▣ 저항 "R"에 발생하는 전압 VR은 처음에는 전압이 모두 "L"에 발생하므로 전압이 발생하
지 않다가 최종적으로 "L"이 단락상태가 되면 모든 전압이 저항 "R"에 발생하게 된다.
【 기전력 인가시 전류 특성 】
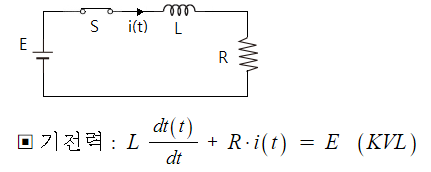
▣ 키르히호프의 전압법칙에 따라 기전력 "E"는 "L"의 전압 VL과 R의 전압 VR의 합과 같다.
※ 위 식은 전류(i)의 특성을 파악하기 위하여 전압을 전류 i(t)의 식을 표현한 것이다.
즉, 미분방정식 ax' + bx = C 를 푸는 방법으로는
① 라플라스 변환을 통해 해를 찾는 방법과
② 미분방정식을 직접 풀어 해를 찾는 방법이 있다.
▣ 먼저 미분방정식을 직접 풀어 보자.


◈ 위의 특성을 이용하여 자연상수 즉 미분을 해도 자기 자신이 되는 함수를 이용하여
위의 식을 풀어 보면 다음과 같은 식이 될 것이라 추정할 수 있다.
⊙ 위에서 is = E / R 라고 구했으므로 i(t)를 구하기 위해 it 를 구해 보자.

▣ it 값을 알기 위해서는 K값을 구해야 한다. 초기값을 즉 it = 0을 이용하여 K값을
구해 보자.

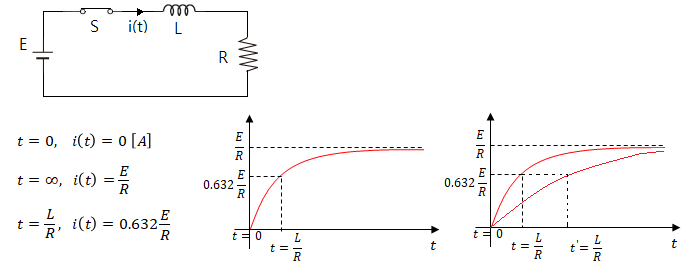
나. 직류 R - L 직렬 회로 시정수
▣ 시정수 : 정상값의 63.2[%]에 도달하는 시간으로 기호로는 τ 를 쓴다.
◈ 시정수 τ = L / R [sec] ⇒ e-1 = 0.632
◈ 시정수가 크면 클 수록 과도현상이 오래 지속된다.
【 전압의 변화 】
▣ 기전력은 E = VR + VL 이다. (키르히호프의 전압법칙)

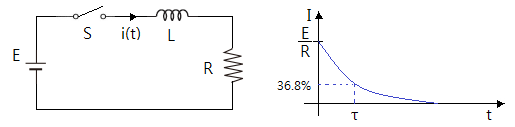
다. 직류 R - L 직렬 회로, 기전력을 제거했을 때
▣ 전류 i(t)의 변화를 알아 보자.

▣ K값을 구하기 위해 초기값을 즉 i(t) = E / R를 이용하여 K값을 구해 보자.

이를 그래프로 나타내면 다음과 같다.
▣ 직류 R-L 직렬회로를 정리하면 다음과 같다.

2. 직류 R - C 직렬회로
▣ 직류 R-C 직렬 회로에서 과도현상에 대하여 알아 보자. 이 때 "C"는 배터리로 생각하면
과도현상을 이해하는데 도움이 된다.
▣ 직류 R-C 직렬 회로에서 전류 I의 흐름은 다음 그림과 같다.
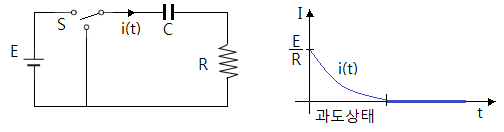
◈ 스위치를 ON 하면 처음에는 기전력과 콘덴서의 전압차이 만큼 전류가 흐르다가 점차
전압차가 줄어 들어 콘덴서가 완전 충전되면 전압차가 같아지고 전류가 흐르지 않는다.
가. 기전력을 인가했을 때
▣ 전류에 대하여 알아 보자.
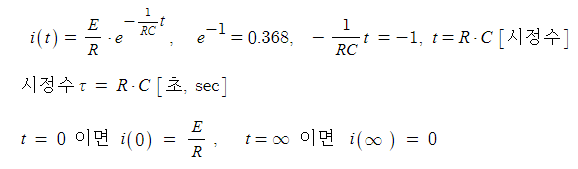
▣ 전압에 대하여 알아 보자.

나. 기전력을 제거했을 때
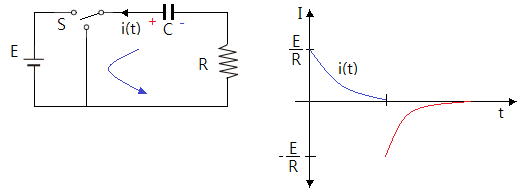
▣ 기전력을 제거하면 콘덴서에 충전되어 있는 전하가 방전을 하게 되어 당초 기전력을
인가했을 때와 반대 방향으로 전류가 흐르게 되며 저항 R에서 에너지를 전부 소모할 때
까지 전류가 흐르며 최종에는 전류가 흐르지 않는다.
◈ 수식으로 보면 다음과 같다.

▣ 전압의 변화를 보면 다음과 같다.
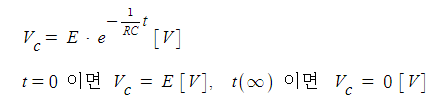
3. 직류 R - L - C 직렬회로
▣ 직류 R-L-C 직렬 회로에서 과도현상은 제동에 관한 사항을 숙지해 두자.
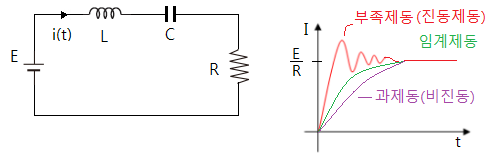
▣ 제동의 종류와 조건식에 대해 알아 보자.

◈ 제동 조건의 변형식을 알아 보자.

4. 직류 L - C 직렬회로
▣ 직류 L-C 직렬 회로에서 과도현상은 충전 - 방전이 반복되는 것을 기억하자.

▣ 직류 L-C 직렬회로에서는 L, C 간에 에너지를 서로 주고 받는 것을 반복한다.
① 불변의 진동 전류가 흐르게 된다.
② 콘덴서 C에 발생하는 전압은 공급전압의 2배가 된다.
즉, Vc = 2 E 가 된다.
'전기이론 > 회로이론' 카테고리의 다른 글
| 동기발전기의 출력 P [W] (0) | 2024.08.21 |
|---|---|
| 전기 회로 이론 : 전달함수 (0) | 2024.08.19 |
| 저항 (R : Resistance) - 회로이론 제2강 (0) | 2024.08.16 |
| 전류와 전압 : 회로이론 제1강 (0) | 2024.08.15 |
| 전기기초이론 - 전류, 전압, 저항, 비정현파(정의, 전압, 전류, 전력 계산) (0) | 2024.08.13 |


