오늘은 전기 회로 이론 중 전달함수에 대해서 알아보자.
전달함수

▣ 전달함수란 ?
◈ 어떤 입력에 대하여 출력을 발생시키는 과정, 어떤 특성을 전달한다는 의미이다.

◈ 어떤 입력값으로 목표로 하는 출력값을 내는 것이 목적이므로 전달함수는 제어계라고도 한다.
X(s) × G(s) = Y(s) 에서 입력 X(s)에 전달함수 G(s)를 곱하여 출력 Y(s)가 된다고 하자.
라플라스로 변환하였기 때문에 곱의 형태로 나타낼 수 있고 라플라스 형태로 표현되었을
때 전달함수라고 하고 라플라스 형태가 아니면 전달함수가 아니다.

▣ 전달함수 정의
⊙ 초기값을 "0"으로 한 상태에서 입력신호와 출력 신호의 라플라스 변환비
※ 라플라스는 "0" → "∞"까지의 변화를 분석하는 것이다.
⊙ 임펄스 입력에 대한 출력의 라플라스 변환 δ(t) = 1
Y(s) = X(s) · G(s)
⊙ 전달함수의 분모 = 0 : 특성방정식
가. 제어요소의 전달함수
▣ 비례요소 : G(s) = K, ▣ 미분요소 : G(s) = S, ▣ 적분요소 G(s) = 1/S
▣ 부동작 요소

▣ 비례요소는 함수에 상수배한 것이다. "K"한 것이다.
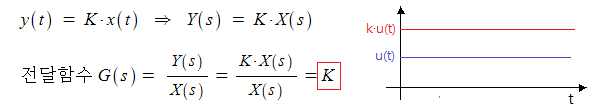
다. 미분요소
▣ 미분의 라플라스 변환은 "S"이고 전달함수도 "S"가 된다.
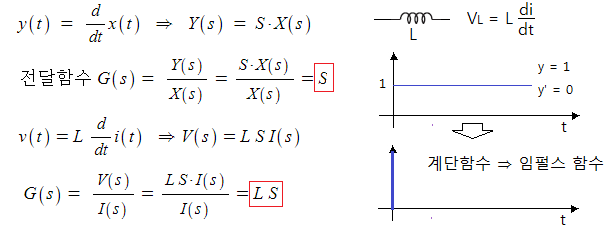
▣ 적분의 라플라스 변환은 "1/S"이고 전달함수도 "1/S"가 된다.
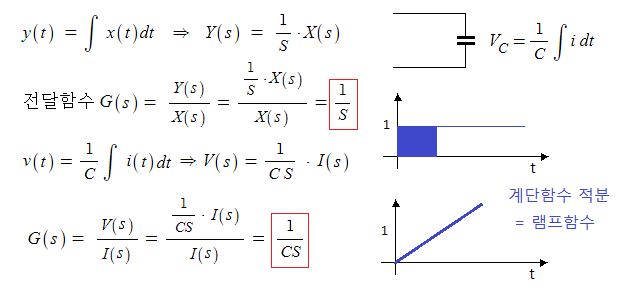
▣ 최종값이 일정 시간 이후에 나타나는 함수 형태이다.

◈ 실제 회로의 예를 보자.
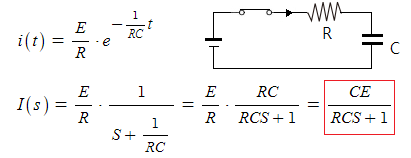
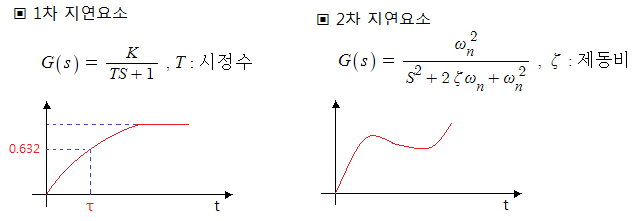
바. 2차 지연요소
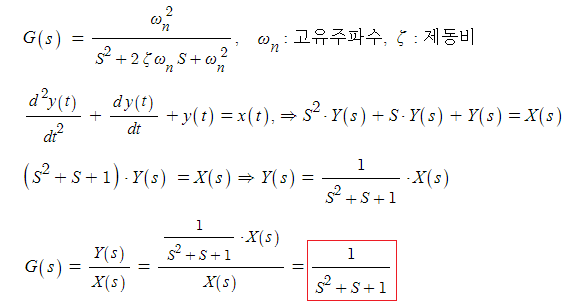
▣ 제동비 : ζ =0 무제동, 0 < ζ < 1 부족제동, ζ = 임계제동, ζ > 1 과제동
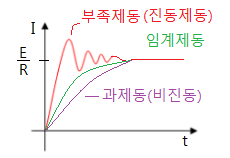
▣ 전기회로에서 2차 지연 요소를 알아 보자.
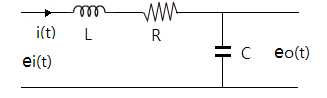
◈ 라플라스 변환하여 전달함수를 구해 보자.

▣ 전류출력을 구하면
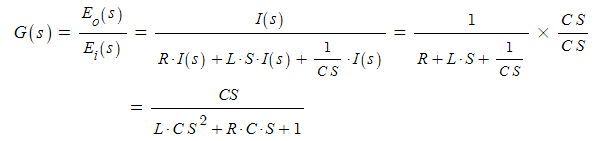
사. 부동작 요소 : Dead time
▣ 부동작 요소는 u(t) 함수의 OFF 상태를 말한다.

【전기회로에서 전달함수】
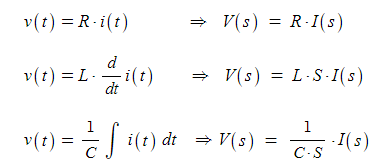
【주어진 조건의 전달함수】

[예1] 전압비는 임피던스 비 이다.
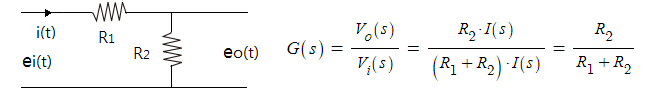
[예2] R-C회로의 1차 지연회로의 예를 보자.

[예3] L-C회로의 2차 지연회로의 예를 보자.

[예4] R-L회로의 1차 지연 미분 회로의 예를 보자.

[예5] R-L-C 회로의 전달함수를 구해보자

[예6] R-L-C 회로의 전달함수를 구해보자

[예7] C-C 회로의 전달함수를 구해보자.
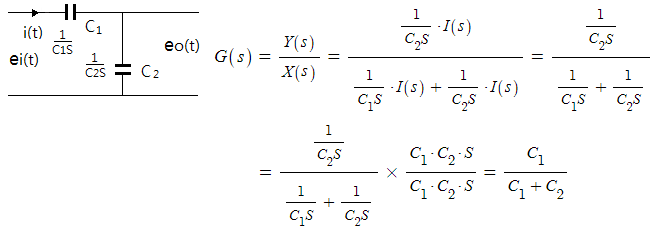
[예8] R-C 회로의 전달함수를 구해보자.
▣ 전압입력에 대한 전류 출력의 전달함수를 구해 보자.
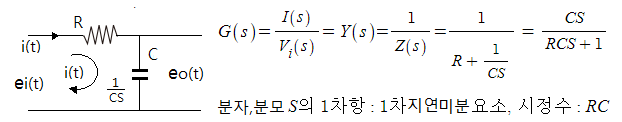
[예9] 미분 방정식의 전달함수를 알아 보자.

[예10] 전달함수에서 원래 방정식 찾기
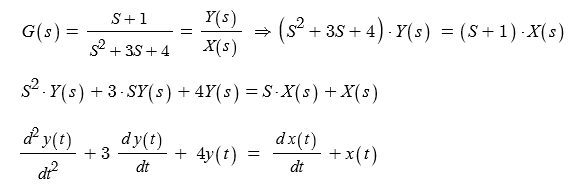
▣ 다음 식의 전달함수를 알아 보자.
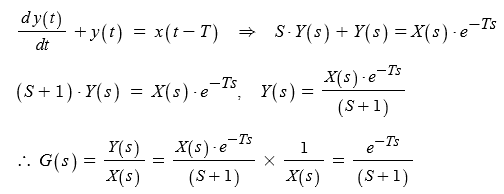
2. 보상회로
▣ 보상회로란 ? 제어계에 순방향 전달함수에 보상요소를 삽입하여 계 전체의 특성을 개선
하는 회로를 말한다.
※ 수동소자의 연결에 따른 진상전류, 지상전류의 발생을 이용한 개념이다.
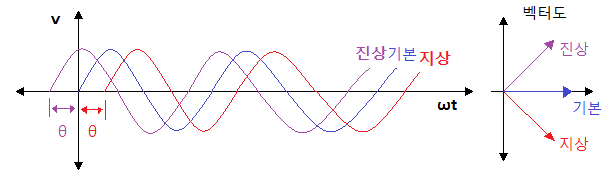
[예1] 다음 회로의 위상 관계(보상관계)를 알아 보자.
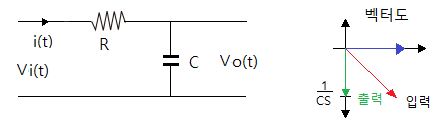
▣ 위 회로는 출력이 입력에 비해 위상이 빠르다. (진상보상 회로)
◈ 입력은 저항과 콘덴서로 이루어져 둘의 합성 위상이 되고 출력은 콘덴서로만 이루어져
저항보다 위상이 90˚ 빠르다.
[예2] 다음 회로의 위상 관계(보상관계)를 알아 보자.
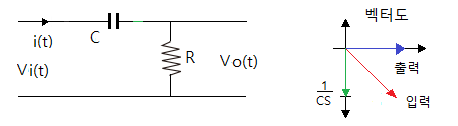
▣ 위 회로는 출력이 입력에 비해 위상이 늦다. (지상보상 회로)
◈ 입력은 저항과 콘덴서로 이루어져 둘의 합성 위상이 되고 출력은 저항만으로 이루어져
콘덴서보다 위상이 90˚ 늦다.
[예3] 다음 R-L회로의 위상 관계(보상관계)를 알아 보자.
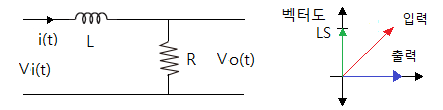
▣ 위 회로는 출력이 입력에 비해 위상이 빠르다. (진상보상 회로)
◈ 입력은 저항과 리액터로 이루어져 둘의 합성 위상이 되고 출력은 저항만으로 이루어져
리액터보다 위상이 90˚ 빠르다.
[예4] 다음 R-C-R 회로의 위상 관계(보상관계)를 알아 보자.

▣ 전달함수를 구해 보자.
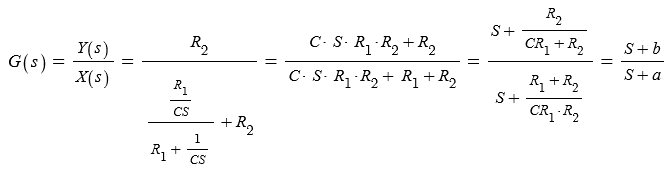
◈ 이 때, a > b 이면, 출력이 입력보다 앞선다. (진상 보상 회로)
[예5] 다음 R-R-C 회로의 위상 관계(보상관계)를 알아 보자.
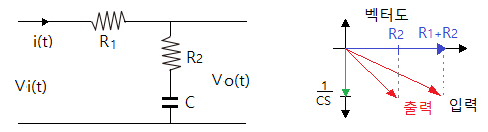
▣ 전달함수를 구해 보자.
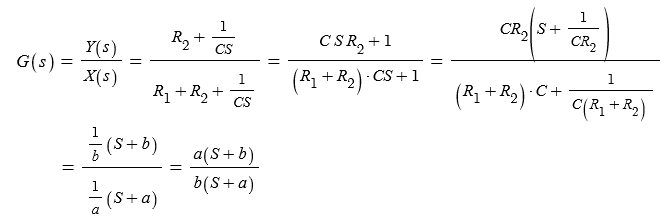
[예6] 다음 R-C-R-C 회로의 위상 관계(보상관계)를 알아 보자.

▣ 전달함수를 구해 보자.

▣ 위 회로는 진,지상보상회로이다.
'전기이론 > 회로이론' 카테고리의 다른 글
| 수하특성(정전류 특성)이란 ? (0) | 2024.08.22 |
|---|---|
| 동기발전기의 출력 P [W] (0) | 2024.08.21 |
| 저항 (R : Resistance) - 회로이론 제2강 (0) | 2024.08.16 |
| 전류와 전압 : 회로이론 제1강 (0) | 2024.08.15 |
| 과도현상 (시정수, 시상수, 특성근) (0) | 2024.08.14 |

